This is a read-only mirror of pymolwiki.org
Difference between revisions of "Kabsch"
(→Notes) |
m (1 revision) |
||
| (24 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <div style="background-color: #9f9; padding: 10px; margin-bottom: 20px"> | ||
| + | '''Note:''' PyMOL has built-in commands to do RMSD fitting. This script is typically not needed. | ||
| + | |||
| + | In particular, <code>optAlign (sele1), (sele2)</code> is identical to <code>fit (sele1), (sele2), matchmaker=-1</code>. | ||
| + | |||
| + | See also: [[fit]], [[align]]. | ||
| + | </div> | ||
| + | |||
| + | {{Infobox script-repo | ||
| + | |type = script | ||
| + | |author = [[User:Inchoate|Jason Vertrees]] | ||
| + | |license = GPL | ||
| + | }} | ||
| + | |||
==Intro== | ==Intro== | ||
The Kabsch algorithm uses linear and vector algebra to find the optimal rotation and translation of two sets of points in N-dimensional space as to minimize the RMSD between them. The following program is a Python implementation of the Kabsch algorithm. | The Kabsch algorithm uses linear and vector algebra to find the optimal rotation and translation of two sets of points in N-dimensional space as to minimize the RMSD between them. The following program is a Python implementation of the Kabsch algorithm. | ||
| Line 4: | Line 18: | ||
This program when called will align the two selections, optimally, convert the proteins in the selection to ribbons and change the color of the selections to show the matched alignments. | This program when called will align the two selections, optimally, convert the proteins in the selection to ribbons and change the color of the selections to show the matched alignments. | ||
| − | '''WHAT THIS DOESN'T DO''': This program does NOT provide a pairwise alignment of two structures from scratch. You have to tell it what the | + | '''WHAT THIS DOESN'T DO''': This program does NOT provide a pairwise alignment of two structures from scratch. You have to tell it what the equivalent items are. See [[Cealign]]. |
| − | '''NOTE:''' This | + | '''NOTE:''' This has '''NOT''' been tested on any other machine than mine, by me. It works on all PyMols 0.97 and newer (haven't tested earlier versions) and I use Python 2.3's Numeric Version 23.3. |
| − | '''NOTE:''' | + | '''NOTE:''' I have added new Kabsch code. The new code uses SVD, and fixed an old bug. For ease of use, try the new code (requires numpy, though). |
==To use== | ==To use== | ||
| Line 20: | Line 34: | ||
To align two equivalent sets of residues do: | To align two equivalent sets of residues do: | ||
<source lang="python"> | <source lang="python"> | ||
| − | optAlign SEL1 and n. CA and i. a-b, SEL2 and n. CA and c-d | + | optAlign SEL1 and n. CA and i. a-b, SEL2 and n. CA and i. c-d |
</source> | </source> | ||
where | where | ||
| Line 31: | Line 45: | ||
* Ensure that you're equivalencing '''N''' atoms to '''N''' atoms (run [[Count_Atoms]] over your two selections to ensure they are the same length). | * Ensure that you're equivalencing '''N''' atoms to '''N''' atoms (run [[Count_Atoms]] over your two selections to ensure they are the same length). | ||
* Sometimes PyMol doesn't seem to superimpose them right the first time. Hit the up-arrow and rerun the program if this happens. It always superimposes the correctly the second time. I think it has something to do with the orientation. I'll fix this when I find the error. | * Sometimes PyMol doesn't seem to superimpose them right the first time. Hit the up-arrow and rerun the program if this happens. It always superimposes the correctly the second time. I think it has something to do with the orientation. I'll fix this when I find the error. | ||
| − | * The RMSD is only between the | + | * The RMSD is only between the equivalent atoms. Use PyMol's [[Rms_Cur]] if you want a full RMSD. |
| − | * Make sure your atom selections are numbered correctly. Many times PDB files start residue numbers at something other than 0 or 1. To ensure you're aligning the right things, do <source lang="python">set seq_view,1</source> to turn on the sequence viewer and double check your residue numbers. If a protein has residue one numbered as something other than one, say 2064, simply run <source lang="python">alter (SEL), resi=str(int(resi)-2064)</source> and then <source lang="python">sort</source> where '''SEL''' is the name of the protein and 2064 is the offset to adjust by. Your protein will now work as needed. See [[Alter]].<br> | + | * Make sure your atom selections are numbered correctly. Many times PDB files start residue numbers at something other than 0 or 1. To ensure you're aligning the right things, do <source lang="python">set seq_view,1</source> to turn on the sequence viewer and double check your residue numbers. If a protein has residue one numbered as something other than one, say 2064, simply run <source lang="python">alter (SEL), resi=str(int(resi)-2064)</source> and then <source lang="python">sort</source> where '''SEL''' is the name of the protein and 2064 is the offset to adjust by. Your protein will now work as needed. See [[Alter]]. This capability is also provided in a script; See [[zero_residues]].<br> |
== Notes == | == Notes == | ||
| Line 44: | Line 58: | ||
optAlign 1kao and n. CA and i. 20-50, 1ctq and n. CA and i. 20-50 | optAlign 1kao and n. CA and i. 20-50, 1ctq and n. CA and i. 20-50 | ||
| − | + | <gallery> | |
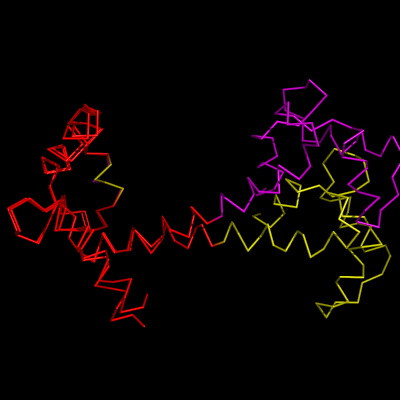
| − | + | Image:OptAlign1.png|1cll and 1ggz loaded | |
| + | Image:OptAlign2.png|1cll and 1ggz aligned to residues 5-50+55-80 shown in red | ||
| + | </gallery> | ||
| − | + | Kabsch can also align hetero-atoms: | |
| − | + | <source lang="python"> | |
| − | + | load 1cll.pdb | |
| − | + | load 1ggz.pdb | |
| − | + | optAlign 1cll and e. CA, 1ggz and e. CA | |
| − | + | </source> | |
| − | + | The above aligns the 4 Calciums in each structure. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==The Code== | ==The Code== | ||
| Line 79: | Line 77: | ||
############################################################################## | ############################################################################## | ||
# | # | ||
| − | # @SUMMARY: -- | + | # @SUMMARY: -- QKabsch.py. A python implementation of the optimal superposition |
# of two sets of vectors as proposed by Kabsch 1976 & 1978. | # of two sets of vectors as proposed by Kabsch 1976 & 1978. | ||
# | # | ||
# @AUTHOR: Jason Vertrees | # @AUTHOR: Jason Vertrees | ||
| − | # @COPYRIGHT: Jason Vertrees ( | + | # @COPYRIGHT: Jason Vertrees (C), 2005-2007 |
| − | # DATE : | + | # @LICENSE: Released under GPL: |
| − | # REV : | + | # This program is free software; you can redistribute it and/or modify |
| + | # it under the terms of the GNU General Public License as published by | ||
| + | # the Free Software Foundation; either version 2 of the License, or | ||
| + | # (at your option) any later version. | ||
| + | # This program is distributed in the hope that it will be useful, but WITHOUT | ||
| + | # ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS | ||
| + | # FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. | ||
| + | # | ||
| + | # You should have received a copy of the GNU General Public License along with | ||
| + | # this program; if not, write to the Free Software Foundation, Inc., 51 Franklin | ||
| + | # Street, Fifth Floor, Boston, MA 02110-1301, USA | ||
| + | # | ||
| + | # DATE : 2007-01-01 | ||
| + | # REV : 2 | ||
| + | # REQUIREMENTS: numpy | ||
# | # | ||
############################################################################# | ############################################################################# | ||
| + | from array import * | ||
| + | |||
| + | # system stuff | ||
| + | import os | ||
| + | import copy | ||
| + | |||
| + | # pretty printing | ||
| + | import pprint | ||
| + | |||
| + | # for importing as a plugin into PyMol | ||
| + | from pymol import cmd | ||
| + | from pymol import stored | ||
| + | from pymol import selector | ||
| + | |||
| + | # using numpy for linear algebra | ||
| + | import numpy | ||
| + | |||
| + | def optAlign( sel1, sel2 ): | ||
| + | """ | ||
| + | optAlign performs the Kabsch alignment algorithm upon the alpha-carbons of two selections. | ||
| + | Example: optAlign MOL1 and i. 20-40, MOL2 and i. 102-122 | ||
| + | Example 2: optAlign 1GGZ and i. 4-146 and n. CA, 1CLL and i. 4-146 and n. CA | ||
| + | |||
| + | Two RMSDs are returned. One comes from the Kabsch algorithm and the other from | ||
| + | PyMol based upon your selections. | ||
| + | |||
| + | By default, this program will optimally align the ALPHA CARBONS of the selections provided. | ||
| + | To turn off this feature remove the lines between the commented "REMOVE ALPHA CARBONS" below. | ||
| + | |||
| + | @param sel1: First PyMol selection with N-atoms | ||
| + | @param sel2: Second PyMol selection with N-atoms | ||
| + | """ | ||
| + | cmd.reset() | ||
| + | |||
| + | # make the lists for holding coordinates | ||
| + | # partial lists | ||
| + | stored.sel1 = [] | ||
| + | stored.sel2 = [] | ||
| + | # full lists | ||
| + | stored.mol1 = [] | ||
| + | stored.mol2 = [] | ||
| + | |||
| + | # -- CUT HERE | ||
| + | sel1 += " and N. CA" | ||
| + | sel2 += " and N. CA" | ||
| + | # -- CUT HERE | ||
| + | |||
| + | # Get the selected coordinates. We | ||
| + | # align these coords. | ||
| + | cmd.iterate_state(1, selector.process(sel1), "stored.sel1.append([x,y,z])") | ||
| + | cmd.iterate_state(1, selector.process(sel2), "stored.sel2.append([x,y,z])") | ||
| + | |||
| + | # get molecule name | ||
| + | mol1 = cmd.identify(sel1,1)[0][0] | ||
| + | mol2 = cmd.identify(sel2,1)[0][0] | ||
| + | |||
| + | # Get all molecule coords. We do this because | ||
| + | # we have to rotate the whole molcule, not just | ||
| + | # the aligned selection | ||
| + | cmd.iterate_state(1, mol1, "stored.mol1.append([x,y,z])") | ||
| + | cmd.iterate_state(1, mol2, "stored.mol2.append([x,y,z])") | ||
| + | |||
| + | # check for consistency | ||
| + | assert len(stored.sel1) == len(stored.sel2) | ||
| + | L = len(stored.sel1) | ||
| + | assert L > 0 | ||
| + | |||
| + | # must alway center the two proteins to avoid | ||
| + | # affine transformations. Center the two proteins | ||
| + | # to their selections. | ||
| + | COM1 = numpy.sum(stored.sel1,axis=0) / float(L) | ||
| + | COM2 = numpy.sum(stored.sel2,axis=0) / float(L) | ||
| + | stored.sel1 -= COM1 | ||
| + | stored.sel2 -= COM2 | ||
| + | |||
| + | # Initial residual, see Kabsch. | ||
| + | E0 = numpy.sum( numpy.sum(stored.sel1 * stored.sel1,axis=0),axis=0) + numpy.sum( numpy.sum(stored.sel2 * stored.sel2,axis=0),axis=0) | ||
| + | |||
| + | # | ||
| + | # This beautiful step provides the answer. V and Wt are the orthonormal | ||
| + | # bases that when multiplied by each other give us the rotation matrix, U. | ||
| + | # S, (Sigma, from SVD) provides us with the error! Isn't SVD great! | ||
| + | V, S, Wt = numpy.linalg.svd( numpy.dot( numpy.transpose(stored.sel2), stored.sel1)) | ||
| + | |||
| + | # we already have our solution, in the results from SVD. | ||
| + | # we just need to check for reflections and then produce | ||
| + | # the rotation. V and Wt are orthonormal, so their det's | ||
| + | # are +/-1. | ||
| + | reflect = float(str(float(numpy.linalg.det(V) * numpy.linalg.det(Wt)))) | ||
| + | |||
| + | if reflect == -1.0: | ||
| + | S[-1] = -S[-1] | ||
| + | V[:,-1] = -V[:,-1] | ||
| + | |||
| + | RMSD = E0 - (2.0 * sum(S)) | ||
| + | RMSD = numpy.sqrt(abs(RMSD / L)) | ||
| + | |||
| + | #U is simply V*Wt | ||
| + | U = numpy.dot(V, Wt) | ||
| + | |||
| + | # rotate and translate the molecule | ||
| + | stored.sel2 = numpy.dot((stored.mol2 - COM2), U) | ||
| + | stored.sel2 = stored.sel2.tolist() | ||
| + | # center the molecule | ||
| + | stored.sel1 = stored.mol1 - COM1 | ||
| + | stored.sel1 = stored.sel1.tolist() | ||
| + | |||
| + | # let PyMol know about the changes to the coordinates | ||
| + | cmd.alter_state(1,mol1,"(x,y,z)=stored.sel1.pop(0)") | ||
| + | cmd.alter_state(1,mol2,"(x,y,z)=stored.sel2.pop(0)") | ||
| + | |||
| + | print("RMSD=%f" % RMSD) | ||
| + | |||
| + | # make the alignment OBVIOUS | ||
| + | cmd.hide('everything') | ||
| + | cmd.show('ribbon', sel1 + ' or ' + sel2) | ||
| + | cmd.color('gray70', mol1 ) | ||
| + | cmd.color('paleyellow', mol2 ) | ||
| + | cmd.color('red', 'visible') | ||
| + | cmd.show('ribbon', 'not visible') | ||
| + | cmd.center('visible') | ||
| + | cmd.orient() | ||
| + | cmd.zoom('visible') | ||
| + | |||
| + | cmd.extend("optAlign", optAlign) | ||
| + | </source> | ||
| + | |||
| + | === The Old Code === | ||
| + | |||
| + | <source lang="python"> | ||
| + | #!python | ||
| + | |||
| + | ############################################################################## | ||
| + | # | ||
| + | # @SUMMARY: -- Kabsch.py. A python implementation of the optimal superposition | ||
| + | # of two sets of vectors as proposed by Kabsch 1976 & 1978. | ||
# | # | ||
| − | # | + | # @AUTHOR: Jason Vertrees |
| − | # | + | # @COPYRIGHT: Jason Vertrees (C), 2005-2007 |
| − | # | + | # @LICENSE: Released under GPL: |
| − | # | + | # This program is free software; you can redistribute it and/or modify |
| + | # it under the terms of the GNU General Public License as published by | ||
| + | # the Free Software Foundation; either version 2 of the License, or | ||
| + | # (at your option) any later version. | ||
| + | # This program is distributed in the hope that it will be useful, but WITHOUT | ||
| + | # ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS | ||
| + | # FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. | ||
# | # | ||
| − | # | + | # You should have received a copy of the GNU General Public License along with |
| − | + | # this program; if not, write to the Free Software Foundation, Inc., 51 Franklin | |
| − | # | + | # Street, Fifth Floor, Boston, MA 02110-1301, USA |
| − | # | ||
| − | |||
# | # | ||
| − | # | + | # DATE : 2005-04-07 |
| − | # | + | # REV : 2 |
| − | # | + | # NOTES: Updated RMSD, notes, cleaned up the code a little. |
# | # | ||
############################################################################# | ############################################################################# | ||
| − | # math | + | # math imports |
import math | import math | ||
import Numeric | import Numeric | ||
import LinearAlgebra | import LinearAlgebra | ||
import Matrix | import Matrix | ||
| − | + | ||
from array import * | from array import * | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
# system stuff | # system stuff | ||
import os | import os | ||
import copy | import copy | ||
| − | + | ||
# pretty printing | # pretty printing | ||
import pprint | import pprint | ||
| − | + | ||
| − | |||
# for importing as a plugin into PyMol | # for importing as a plugin into PyMol | ||
#import tkSimpleDialog | #import tkSimpleDialog | ||
| Line 130: | Line 278: | ||
from pymol import stored | from pymol import stored | ||
from pymol import selector | from pymol import selector | ||
| − | + | ||
class kabsch: | class kabsch: | ||
""" | """ | ||
| − | Kabsch alignment of two set of vectors to produce and optimal | + | Kabsch alignment of two set of vectors to produce and optimal alignment. |
| − | + | ||
Steps | Steps | ||
===== | ===== | ||
| Line 188: | Line 336: | ||
Coordinates should be formatted as as array of 2D vectors/lists. | Coordinates should be formatted as as array of 2D vectors/lists. | ||
| − | + | ||
""" | """ | ||
| Line 194: | Line 342: | ||
def __init__(self): | def __init__(self): | ||
""" | """ | ||
| − | Constructor | + | Constructor. @see kabsch.align. |
""" | """ | ||
| − | + | ||
# | # | ||
# Instance Variables: All three of these will be updated | # Instance Variables: All three of these will be updated | ||
| Line 208: | Line 356: | ||
# R, the RMSD | # R, the RMSD | ||
self.R = -1.0 | self.R = -1.0 | ||
| − | + | ||
#self.menuBar.addmenuitem('Plugin', 'command', 'Kabsch Align', label = "Align Selections to Optial RMSD", command = lamda s=self: fetchPDBDialog(s)) | #self.menuBar.addmenuitem('Plugin', 'command', 'Kabsch Align', label = "Align Selections to Optial RMSD", command = lamda s=self: fetchPDBDialog(s)) | ||
| Line 216: | Line 364: | ||
Finds the best alignment of c1 and c2's pairs resulting in | Finds the best alignment of c1 and c2's pairs resulting in | ||
the smallest possible RMSD. | the smallest possible RMSD. | ||
| − | + | ||
@note: | @note: | ||
| Line 262: | Line 410: | ||
U = self.calcU(eVectors, bVectors) | U = self.calcU(eVectors, bVectors) | ||
# Calculate the final RMSD using U. | # Calculate the final RMSD using U. | ||
| − | RMSD = self.calcRMSD(E0, eValues, eVectors, bVectors, R) | + | RMSD = self.calcRMSD(E0, eValues, eVectors, bVectors, R, len(c1)) |
return U, T1, T2, RMSD, c1, c2 | return U, T1, T2, RMSD, c1, c2 | ||
| Line 291: | Line 439: | ||
# make sure we don't get bad data | # make sure we don't get bad data | ||
| − | assert | + | if len(c1) != len(c2): |
| − | + | print "Two different length selections, with lengths, %d and %d." % (len(c1), len(c2)) | |
| + | print "This algorithm must be used with selections of the same length." | ||
| + | print "In PyMol, type 'count_atoms sel1' where sel1 are your selections to find out their lengths." | ||
| + | print "Example: optAlign MOL1 and i. 20-40, MOL2 and i. 102-122" | ||
| + | print "Example 2: optAlign 1GGZ and i. 4-146 and n. CA, 1CLL and i. 4-146 and n. CA" | ||
| + | |||
| + | |||
| + | assert len(c1) == len(c2) != 0 | ||
| + | |||
L = len(c1) | L = len(c1) | ||
| Line 300: | Line 456: | ||
c1COM = Numeric.zeros((3,1), Numeric.Float64) | c1COM = Numeric.zeros((3,1), Numeric.Float64) | ||
c2COM = Numeric.zeros((3,1), Numeric.Float64) | c2COM = Numeric.zeros((3,1), Numeric.Float64) | ||
| − | + | ||
# calculate the CsOM | # calculate the CsOM | ||
| − | for i in range( | + | for i in range(L): |
| − | for j in range( | + | for j in range(3): |
| − | c1COM[j] = | + | c1COM[j] += c1[i][j] |
| − | c2COM[j] = | + | c2COM[j] += c2[i][j] |
T1 = - c1COM / L | T1 = - c1COM / L | ||
T2 = - c2COM / L | T2 = - c2COM / L | ||
| − | + | ||
# move everything back to the origin. | # move everything back to the origin. | ||
| − | for i in range( | + | for i in range(L): |
| − | for j in range( | + | for j in range(3): |
| − | c1[i][j] = | + | c1[i][j] += T1[j] |
| − | c2[i][j] = | + | c2[i][j] += T2[j] |
return T1, T2, c1, c2 | return T1, T2, c1, c2 | ||
| − | + | ||
def calcR( self, c1, c2 ): | def calcR( self, c1, c2 ): | ||
| Line 325: | Line 481: | ||
(CORRECT) | (CORRECT) | ||
| − | @param c1: | + | @param c1: coordinates of the first vectors, as an array of 3D vectors. |
@type c1: Python list | @type c1: Python list | ||
@param c2: coordinates of the second set of vectors, as an array of 3D vectors. | @param c2: coordinates of the second set of vectors, as an array of 3D vectors. | ||
@type c2: Python list | @type c2: Python list | ||
| − | + | ||
@postcondition: R is now defined. | @postcondition: R is now defined. | ||
| Line 342: | Line 498: | ||
L = len(c1) | L = len(c1) | ||
| − | for k in range( | + | for k in range(L): |
| − | for i in range( | + | for i in range(3): |
| − | for j in range( | + | for j in range(3): |
| − | + | R[i][j] += c2[k][i] * c1[k][j] | |
| − | R[i][j] = | ||
# return R the 3x3 PSD Matrix. | # return R the 3x3 PSD Matrix. | ||
| Line 367: | Line 522: | ||
""" | """ | ||
| − | + | ||
| − | + | RtR = Numeric.matrixmultiply(Numeric.transpose(R), R) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | RtR = Numeric. | ||
return RtR | return RtR | ||
| Line 382: | Line 532: | ||
Calculate the corresponding eigenpairs for RtR, and sort them accordingly: | Calculate the corresponding eigenpairs for RtR, and sort them accordingly: | ||
M{m1 >= m2 >= m3}; set M{v3 = v1 x v2} to ensure a RHS | M{m1 >= m2 >= m3}; set M{v3 = v1 x v2} to ensure a RHS | ||
| − | (CORRECT | + | (CORRECT) |
@postcondition: The eigen pairs are calculated, sorted such that M{m1 >= m2 >= m3} and | @postcondition: The eigen pairs are calculated, sorted such that M{m1 >= m2 >= m3} and | ||
| Line 395: | Line 545: | ||
eVal, eVec = LinearAlgebra.eigenvectors(RtR) | eVal, eVec = LinearAlgebra.eigenvectors(RtR) | ||
| − | + | ||
# This is cool. We sort it using Numeric.sort(eVal) | # This is cool. We sort it using Numeric.sort(eVal) | ||
# then we reverse it using nifty-crazy ass notation [::-1]. | # then we reverse it using nifty-crazy ass notation [::-1]. | ||
| Line 402: | Line 552: | ||
# Map the vectors to their appropriate owners | # Map the vectors to their appropriate owners | ||
| − | if | + | if eVal2[0] == eVal[0]: |
eVec2[0] = eVec[0] | eVec2[0] = eVec[0] | ||
| − | if | + | if eVal2[1] == eVal[1]: |
eVec2[1] = eVec[1] | eVec2[1] = eVec[1] | ||
eVec2[2] = eVec[2] | eVec2[2] = eVec[2] | ||
| Line 410: | Line 560: | ||
eVec2[1] = eVec[2] | eVec2[1] = eVec[2] | ||
eVec2[2] = eVec[1] | eVec2[2] = eVec[1] | ||
| − | elif | + | elif eVal2[0] == eVal[1]: |
eVec2[0] = eVec[1] | eVec2[0] = eVec[1] | ||
| − | if | + | if eVal2[1] == eVal[0]: |
eVec2[1] = eVec[0] | eVec2[1] = eVec[0] | ||
eVec2[2] = eVec[2] | eVec2[2] = eVec[2] | ||
| Line 418: | Line 568: | ||
eVec2[1] = eVec[2] | eVec2[1] = eVec[2] | ||
eVec2[2] = eVec[0] | eVec2[2] = eVec[0] | ||
| − | elif | + | elif eVal2[0] == eVal[2]: |
eVec2[0] = eVec[2] | eVec2[0] = eVec[2] | ||
| − | if | + | if eVal2[1] == eVal[1]: |
eVec2[1] = eVec[1] | eVec2[1] = eVec[1] | ||
eVec2[2] = eVec[0] | eVec2[2] = eVec[0] | ||
| Line 426: | Line 576: | ||
eVec2[1] = eVec[0] | eVec2[1] = eVec[0] | ||
eVec2[2] = eVec[1] | eVec2[2] = eVec[1] | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
eVec2[2][0] = eVec2[0][1]*eVec2[1][2] - eVec2[0][2]*eVec2[1][1] | eVec2[2][0] = eVec2[0][1]*eVec2[1][2] - eVec2[0][2]*eVec2[1][1] | ||
eVec2[2][1] = eVec2[0][2]*eVec2[1][0] - eVec2[0][0]*eVec2[1][2] | eVec2[2][1] = eVec2[0][2]*eVec2[1][0] - eVec2[0][0]*eVec2[1][2] | ||
eVec2[2][2] = eVec2[0][0]*eVec2[1][1] - eVec2[0][1]*eVec2[1][0] | eVec2[2][2] = eVec2[0][0]*eVec2[1][1] - eVec2[0][1]*eVec2[1][0] | ||
| − | |||
return [eVal2, eVec2] | return [eVal2, eVec2] | ||
| Line 451: | Line 597: | ||
bVectors = Numeric.zeros((3,3), Numeric.Float64) | bVectors = Numeric.zeros((3,3), Numeric.Float64) | ||
| − | + | ||
| − | for i in range( | + | for i in range(3): |
bVectors[i] = Numeric.matrixmultiply(R, eVectors[i]) | bVectors[i] = Numeric.matrixmultiply(R, eVectors[i]) | ||
| − | + | ||
| − | |||
bVectors[0] = bVectors[0] / Numeric.sqrt(Numeric.add.reduce(bVectors[0]**2)) | bVectors[0] = bVectors[0] / Numeric.sqrt(Numeric.add.reduce(bVectors[0]**2)) | ||
bVectors[1] = bVectors[1] / Numeric.sqrt(Numeric.add.reduce(bVectors[1]**2)) | bVectors[1] = bVectors[1] / Numeric.sqrt(Numeric.add.reduce(bVectors[1]**2)) | ||
bVectors[2] = bVectors[2] / Numeric.sqrt(Numeric.add.reduce(bVectors[2]**2)) | bVectors[2] = bVectors[2] / Numeric.sqrt(Numeric.add.reduce(bVectors[2]**2)) | ||
| − | |||
| − | |||
| − | |||
bVectors[2][0] = bVectors[0][1]*bVectors[1][2] - bVectors[0][2]*bVectors[1][1] | bVectors[2][0] = bVectors[0][1]*bVectors[1][2] - bVectors[0][2]*bVectors[1][1] | ||
bVectors[2][1] = bVectors[0][2]*bVectors[1][0] - bVectors[0][0]*bVectors[1][2] | bVectors[2][1] = bVectors[0][2]*bVectors[1][0] - bVectors[0][0]*bVectors[1][2] | ||
bVectors[2][2] = bVectors[0][0]*bVectors[1][1] - bVectors[0][1]*bVectors[1][0] | bVectors[2][2] = bVectors[0][0]*bVectors[1][1] - bVectors[0][1]*bVectors[1][0] | ||
| − | |||
| − | |||
return bVectors | return bVectors | ||
| Line 494: | Line 634: | ||
U = Numeric.zeros((3,3), Numeric.Float64) | U = Numeric.zeros((3,3), Numeric.Float64) | ||
| − | for k in range( | + | for k in range(3): |
| − | for i in range( | + | for i in range(3): |
| − | for j in range( | + | for j in range(3): |
| − | U[i][j] = | + | U[i][j] += Numeric.matrixmultiply(bVectors[k][i], eVectors[k][j]) |
return U | return U | ||
| Line 504: | Line 644: | ||
def calcE0( self, c1, c2 ): | def calcE0( self, c1, c2 ): | ||
""" | """ | ||
| − | Calculates the initial RMSD, which | + | Calculates the initial RMSD, which Kacbsch called E0. |
(CORRECT) | (CORRECT) | ||
| Line 521: | Line 661: | ||
L = len(c1) | L = len(c1) | ||
| − | for i in range( | + | for i in range( L ): |
| − | for j in range( | + | for j in range(3): |
| − | E0 = | + | E0 += 0.5*( c1[i][j]*c1[i][j]+c2[i][j]*c2[i][j]) |
return E0 | return E0 | ||
| − | def calcRMSD( self, E0, eValues, eVectors, bVectors, R): | + | def calcRMSD( self, E0, eValues, eVectors, bVectors, R, N): |
""" | """ | ||
Calculate the RMSD. The residual error is then | Calculate the RMSD. The residual error is then | ||
| Line 543: | Line 683: | ||
@param R: The matrix R, from L{calcR}. | @param R: The matrix R, from L{calcR}. | ||
@type R: 3x3 matrix. | @type R: 3x3 matrix. | ||
| + | |||
| + | @param N: Number of equivalenced points | ||
| + | @type N: integer | ||
@postcondition: RMSD is computed. | @postcondition: RMSD is computed. | ||
| Line 549: | Line 692: | ||
""" | """ | ||
sigma3 = 0 | sigma3 = 0 | ||
| − | if | + | if Numeric.matrixmultiply(bVectors[2], Numeric.matrixmultiply( R, eVectors[2])) < 0: |
sigma3 = -1 | sigma3 = -1 | ||
else: | else: | ||
sigma3 = 1 | sigma3 = 1 | ||
| − | + | ||
| − | E = E0 - math.sqrt(eValues[0]) - math.sqrt(eValues[1]) - sigma3*(math.sqrt(eValues[2])) | + | E = math.sqrt( 2*(E0 - math.sqrt(eValues[0]) - math.sqrt(eValues[1]) - sigma3*(math.sqrt(eValues[2]))) / N) |
return E | return E | ||
| Line 576: | Line 719: | ||
RMSD = 0.0 | RMSD = 0.0 | ||
| − | for i in range( | + | for i in range(len(c1)): |
| − | for j in range( | + | for j in range(3): |
| − | RMSD = | + | RMSD += (c2[i][j]-c1[i][j])**2 |
RMSD = RMSD / len(c1) | RMSD = RMSD / len(c1) | ||
| Line 585: | Line 728: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
##################################################################### | ##################################################################### | ||
# | # | ||
| Line 618: | Line 746: | ||
L = len(c2) | L = len(c2) | ||
| − | + | ||
| − | for n in range( | + | for n in range(L): |
c2[n][0] = c2[n][0] * U[0][0] + c2[n][1] * U[1][0] + c2[n][2] * U[2][0] | c2[n][0] = c2[n][0] * U[0][0] + c2[n][1] * U[1][0] + c2[n][2] * U[2][0] | ||
c2[n][1] = c2[n][0] * U[0][1] + c2[n][1] * U[1][1] + c2[n][2] * U[2][1] | c2[n][1] = c2[n][0] * U[0][1] + c2[n][1] * U[1][1] + c2[n][2] * U[2][1] | ||
| Line 632: | Line 760: | ||
""" | """ | ||
| − | if | + | if len(fileName) == 0: |
fileName = "./U" | fileName = "./U" | ||
outFile = open( fileName, "wb") | outFile = open( fileName, "wb") | ||
| − | for i in range( | + | for i in range(3): |
| − | for j in range( | + | for j in range(3): |
| − | outFile.write | + | outFile.write( str(U[i][j]).ljust(20) ) |
outFile.write("\n") | outFile.write("\n") | ||
outFile.close() | outFile.close() | ||
| − | + | ||
| + | |||
def optAlign( sel1, sel2 ): | def optAlign( sel1, sel2 ): | ||
""" | """ | ||
| − | optAlign | + | optAlign performs the Kabsch alignment algorithm upon the alpha-carbons of two selections. |
| − | + | Example: optAlign MOL1 and i. 20-40, MOL2 and i. 102-122 | |
| − | + | Example 2: optAlign 1GGZ and i. 4-146 and n. CA, 1CLL and i. 4-146 and n. CA | |
| − | + | ||
| − | + | Two RMSDs are returned. One comes from the Kabsch algorithm and the other from | |
| + | PyMol based upon your selections. | ||
| + | |||
| + | By default, this program will optimally align the ALPHA CARBONS of the selections provided. | ||
| + | To turn off this feature remove the lines between the commented "REMOVE ALPHA CARBONS" below. | ||
@param sel1: First PyMol selection with N-atoms | @param sel1: First PyMol selection with N-atoms | ||
| Line 655: | Line 788: | ||
""" | """ | ||
cmd.reset() | cmd.reset() | ||
| − | + | ||
# make the lists for holding coordinates | # make the lists for holding coordinates | ||
# partial lists | # partial lists | ||
| Line 663: | Line 796: | ||
stored.mol1 = [] | stored.mol1 = [] | ||
stored.mol2 = [] | stored.mol2 = [] | ||
| − | + | ||
# now put the coordinates into a list | # now put the coordinates into a list | ||
# partials | # partials | ||
| + | |||
| + | # -- REMOVE ALPHA CARBONS | ||
| + | sel1 += " and N. CA" | ||
| + | sel2 += " and N. CA" | ||
| + | # -- REMOVE ALPHA CARBONS | ||
| + | |||
cmd.iterate_state(1, selector.process(sel1), "stored.sel1.append([x,y,z])") | cmd.iterate_state(1, selector.process(sel1), "stored.sel1.append([x,y,z])") | ||
cmd.iterate_state(1, selector.process(sel2), "stored.sel2.append([x,y,z])") | cmd.iterate_state(1, selector.process(sel2), "stored.sel2.append([x,y,z])") | ||
| Line 673: | Line 812: | ||
cmd.iterate_state(1, mol1, "stored.mol1.append([x,y,z])") | cmd.iterate_state(1, mol1, "stored.mol1.append([x,y,z])") | ||
cmd.iterate_state(1, mol2, "stored.mol2.append([x,y,z])") | cmd.iterate_state(1, mol2, "stored.mol2.append([x,y,z])") | ||
| − | + | ||
K = kabsch() | K = kabsch() | ||
U, T1, T2, RMSD, c1, c2 = K.align(stored.sel1, stored.sel2, []) | U, T1, T2, RMSD, c1, c2 = K.align(stored.sel1, stored.sel2, []) | ||
| − | + | ||
| − | + | stored.mol2 = map(lambda v:[T2[0]+((v[0]*U[0][0])+(v[1]*U[1][0])+(v[2]*U[2][0])),T2[1]+((v[0]*U[0][1])+(v[1]*U[1][1])+(v[2]*U[2][1])),T2[2]+((v[0]*U[0][2])+(v[1]*U[1][2])+(v[2]*U[2][2]))],stored.mol2) | |
| − | + | #stored.mol1 = map(lambda v:[ v[0]+T1[0], v[1]+T1[1], v[2]+T1[2] ], stored.mol1) | |
| − | stored.mol2 = map(lambda v:[ T2[0]+((v[0]*U[0][0])+(v[1]*U[1][0])+(v[2]*U[2][0])), T2[1]+((v[0]*U[0][1])+(v[1]*U[1][1])+(v[2]*U[2][1])), T2[2]+((v[0]*U[0][2])+(v[1]*U[1][2])+(v[2]*U[2][2])) ], stored.mol2) | ||
| − | |||
stored.mol1 = map(lambda v:[ v[0]+T1[0], v[1]+T1[1], v[2]+T1[2] ], stored.mol1) | stored.mol1 = map(lambda v:[ v[0]+T1[0], v[1]+T1[1], v[2]+T1[2] ], stored.mol1) | ||
| − | + | ||
| − | + | cmd.alter_state(1,mol1,"(x,y,z)=stored.mol1.pop(0)") | |
| − | cmd.alter_state(1,mol1,"(x,y,z)= | + | cmd.alter_state(1,mol2,"(x,y,z)=stored.mol2.pop(0)") |
| − | cmd.alter_state(1,mol2,"(x,y,z)= | + | cmd.alter( 'all',"segi=''") |
| − | + | cmd.alter('all', "chain=''") | |
| − | + | print "RMSD=%f" % cmd.rms_cur(sel1, sel2) | |
| − | print "RMSD=%f" % RMSD | + | print "MY RMSD=%f" % RMSD |
| − | |||
cmd.hide('everything') | cmd.hide('everything') | ||
cmd.show('ribbon', sel1 + ' or ' + sel2) | cmd.show('ribbon', sel1 + ' or ' + sel2) | ||
| − | cmd.color(' | + | cmd.color('gray70', mol1 ) |
| − | cmd.color(' | + | cmd.color('paleyellow', mol2 ) |
cmd.color('red', 'visible') | cmd.color('red', 'visible') | ||
cmd.show('ribbon', 'not visible') | cmd.show('ribbon', 'not visible') | ||
| Line 699: | Line 835: | ||
cmd.orient() | cmd.orient() | ||
cmd.zoom('visible') | cmd.zoom('visible') | ||
| − | + | ||
| − | cmd.extend("optAlign", optAlign) | + | cmd.extend("optAlign", optAlign) |
</source> | </source> | ||
| Line 714: | Line 850: | ||
[[Category:Script_Library|Kabsch Alignment]] | [[Category:Script_Library|Kabsch Alignment]] | ||
| + | [[Category:Structure_Alignment|Kabsch Alignment]] | ||
Latest revision as of 03:23, 29 April 2019
Note: PyMOL has built-in commands to do RMSD fitting. This script is typically not needed.
In particular, optAlign (sele1), (sele2) is identical to fit (sele1), (sele2), matchmaker=-1.
| Type | Python Script |
|---|---|
| Download | |
| Author(s) | Jason Vertrees |
| License | GPL |
Intro
The Kabsch algorithm uses linear and vector algebra to find the optimal rotation and translation of two sets of points in N-dimensional space as to minimize the RMSD between them. The following program is a Python implementation of the Kabsch algorithm.
This program when called will align the two selections, optimally, convert the proteins in the selection to ribbons and change the color of the selections to show the matched alignments.
WHAT THIS DOESN'T DO: This program does NOT provide a pairwise alignment of two structures from scratch. You have to tell it what the equivalent items are. See Cealign.
NOTE: This has NOT been tested on any other machine than mine, by me. It works on all PyMols 0.97 and newer (haven't tested earlier versions) and I use Python 2.3's Numeric Version 23.3.
NOTE: I have added new Kabsch code. The new code uses SVD, and fixed an old bug. For ease of use, try the new code (requires numpy, though).
To use
- Save this script to Kabsch.py
- Open PyMol
- Load the alignment script: run Kabsch.py (The command optAlign is now defined in PyMol.)
- Load your proteins
- Align the proper segments (see below examples)
To align two equivalent sets of residues do:
optAlign SEL1 and n. CA and i. a-b, SEL2 and n. CA and i. c-d
where
- SEL1 is the first protein
- a-b is the range of residues to align in the first protein
- SEL2 is the second protein
- c-d is the range of residues to align in the second protein
Caveats
- Ensure that you're equivalencing N atoms to N atoms (run Count_Atoms over your two selections to ensure they are the same length).
- Sometimes PyMol doesn't seem to superimpose them right the first time. Hit the up-arrow and rerun the program if this happens. It always superimposes the correctly the second time. I think it has something to do with the orientation. I'll fix this when I find the error.
- The RMSD is only between the equivalent atoms. Use PyMol's Rms_Cur if you want a full RMSD.
- Make sure your atom selections are numbered correctly. Many times PDB files start residue numbers at something other than 0 or 1. To ensure you're aligning the right things, do to turn on the sequence viewer and double check your residue numbers. If a protein has residue one numbered as something other than one, say 2064, simply run
set seq_view,1
and thenalter (SEL), resi=str(int(resi)-2064)
where SEL is the name of the protein and 2064 is the offset to adjust by. Your protein will now work as needed. See Alter. This capability is also provided in a script; See zero_residues.sort
Notes
- Windows users are having problems running the script. Python tells them first off "TypeError: Can't convert rank-0 arrays to Python scalars." The fix to that breaks some code in Numeric -- which I don't maintain.
- However, to make this work, you can change the code in Numeric.py supplied with Pymol, located in the folder "<Pymol Home>\modules\Numeric\" (for example: "C:\Program Files\DeLano Scientific\PyMOL\modules\Numeric").
Essentially, you need to search for the line:and replace it with:if axis2 < 0: axis2 = axis1 + n # (should be around line 250)
if axis2 < 0: axis2 = axis2 + n
Examples
optAlign 1cll and n. CA and i. 4-20+30-60, 1ggz and n. CA and i. 4-20+30-60
optAlign 1kao and n. CA and i. 20-50, 1ctq and n. CA and i. 20-50
Kabsch can also align hetero-atoms:
load 1cll.pdb
load 1ggz.pdb
optAlign 1cll and e. CA, 1ggz and e. CA
The above aligns the 4 Calciums in each structure.
The Code
#!python
##############################################################################
#
# @SUMMARY: -- QKabsch.py. A python implementation of the optimal superposition
# of two sets of vectors as proposed by Kabsch 1976 & 1978.
#
# @AUTHOR: Jason Vertrees
# @COPYRIGHT: Jason Vertrees (C), 2005-2007
# @LICENSE: Released under GPL:
# This program is free software; you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation; either version 2 of the License, or
# (at your option) any later version.
# This program is distributed in the hope that it will be useful, but WITHOUT
# ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS
# FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
#
# You should have received a copy of the GNU General Public License along with
# this program; if not, write to the Free Software Foundation, Inc., 51 Franklin
# Street, Fifth Floor, Boston, MA 02110-1301, USA
#
# DATE : 2007-01-01
# REV : 2
# REQUIREMENTS: numpy
#
#############################################################################
from array import *
# system stuff
import os
import copy
# pretty printing
import pprint
# for importing as a plugin into PyMol
from pymol import cmd
from pymol import stored
from pymol import selector
# using numpy for linear algebra
import numpy
def optAlign( sel1, sel2 ):
"""
optAlign performs the Kabsch alignment algorithm upon the alpha-carbons of two selections.
Example: optAlign MOL1 and i. 20-40, MOL2 and i. 102-122
Example 2: optAlign 1GGZ and i. 4-146 and n. CA, 1CLL and i. 4-146 and n. CA
Two RMSDs are returned. One comes from the Kabsch algorithm and the other from
PyMol based upon your selections.
By default, this program will optimally align the ALPHA CARBONS of the selections provided.
To turn off this feature remove the lines between the commented "REMOVE ALPHA CARBONS" below.
@param sel1: First PyMol selection with N-atoms
@param sel2: Second PyMol selection with N-atoms
"""
cmd.reset()
# make the lists for holding coordinates
# partial lists
stored.sel1 = []
stored.sel2 = []
# full lists
stored.mol1 = []
stored.mol2 = []
# -- CUT HERE
sel1 += " and N. CA"
sel2 += " and N. CA"
# -- CUT HERE
# Get the selected coordinates. We
# align these coords.
cmd.iterate_state(1, selector.process(sel1), "stored.sel1.append([x,y,z])")
cmd.iterate_state(1, selector.process(sel2), "stored.sel2.append([x,y,z])")
# get molecule name
mol1 = cmd.identify(sel1,1)[0][0]
mol2 = cmd.identify(sel2,1)[0][0]
# Get all molecule coords. We do this because
# we have to rotate the whole molcule, not just
# the aligned selection
cmd.iterate_state(1, mol1, "stored.mol1.append([x,y,z])")
cmd.iterate_state(1, mol2, "stored.mol2.append([x,y,z])")
# check for consistency
assert len(stored.sel1) == len(stored.sel2)
L = len(stored.sel1)
assert L > 0
# must alway center the two proteins to avoid
# affine transformations. Center the two proteins
# to their selections.
COM1 = numpy.sum(stored.sel1,axis=0) / float(L)
COM2 = numpy.sum(stored.sel2,axis=0) / float(L)
stored.sel1 -= COM1
stored.sel2 -= COM2
# Initial residual, see Kabsch.
E0 = numpy.sum( numpy.sum(stored.sel1 * stored.sel1,axis=0),axis=0) + numpy.sum( numpy.sum(stored.sel2 * stored.sel2,axis=0),axis=0)
#
# This beautiful step provides the answer. V and Wt are the orthonormal
# bases that when multiplied by each other give us the rotation matrix, U.
# S, (Sigma, from SVD) provides us with the error! Isn't SVD great!
V, S, Wt = numpy.linalg.svd( numpy.dot( numpy.transpose(stored.sel2), stored.sel1))
# we already have our solution, in the results from SVD.
# we just need to check for reflections and then produce
# the rotation. V and Wt are orthonormal, so their det's
# are +/-1.
reflect = float(str(float(numpy.linalg.det(V) * numpy.linalg.det(Wt))))
if reflect == -1.0:
S[-1] = -S[-1]
V[:,-1] = -V[:,-1]
RMSD = E0 - (2.0 * sum(S))
RMSD = numpy.sqrt(abs(RMSD / L))
#U is simply V*Wt
U = numpy.dot(V, Wt)
# rotate and translate the molecule
stored.sel2 = numpy.dot((stored.mol2 - COM2), U)
stored.sel2 = stored.sel2.tolist()
# center the molecule
stored.sel1 = stored.mol1 - COM1
stored.sel1 = stored.sel1.tolist()
# let PyMol know about the changes to the coordinates
cmd.alter_state(1,mol1,"(x,y,z)=stored.sel1.pop(0)")
cmd.alter_state(1,mol2,"(x,y,z)=stored.sel2.pop(0)")
print("RMSD=%f" % RMSD)
# make the alignment OBVIOUS
cmd.hide('everything')
cmd.show('ribbon', sel1 + ' or ' + sel2)
cmd.color('gray70', mol1 )
cmd.color('paleyellow', mol2 )
cmd.color('red', 'visible')
cmd.show('ribbon', 'not visible')
cmd.center('visible')
cmd.orient()
cmd.zoom('visible')
cmd.extend("optAlign", optAlign)
The Old Code
#!python
##############################################################################
#
# @SUMMARY: -- Kabsch.py. A python implementation of the optimal superposition
# of two sets of vectors as proposed by Kabsch 1976 & 1978.
#
# @AUTHOR: Jason Vertrees
# @COPYRIGHT: Jason Vertrees (C), 2005-2007
# @LICENSE: Released under GPL:
# This program is free software; you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation; either version 2 of the License, or
# (at your option) any later version.
# This program is distributed in the hope that it will be useful, but WITHOUT
# ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS
# FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
#
# You should have received a copy of the GNU General Public License along with
# this program; if not, write to the Free Software Foundation, Inc., 51 Franklin
# Street, Fifth Floor, Boston, MA 02110-1301, USA
#
# DATE : 2005-04-07
# REV : 2
# NOTES: Updated RMSD, notes, cleaned up the code a little.
#
#############################################################################
# math imports
import math
import Numeric
import LinearAlgebra
import Matrix
from array import *
# system stuff
import os
import copy
# pretty printing
import pprint
# for importing as a plugin into PyMol
#import tkSimpleDialog
#import tkMessageBox
from pymol import cmd
from pymol import stored
from pymol import selector
class kabsch:
"""
Kabsch alignment of two set of vectors to produce and optimal alignment.
Steps
=====
1. Calculate the center of mass for each protein. Then, move the protein
to its center of mass. We choose as a convention, to use the origin as
the center of mass of the first set of coordinates. This will allow us to
return one translation vector, instead of two.
Update: Since any rotation around a point that's not the origin, is in fact
an affine rotation. So, to beat that, we translate both to the center.
NAME: superpose(c1, c2)
POST: T is now defined.
2. Calculate the matrix, R, by (eq7, 1976). r_{i,j} = sum_n w_n * y_{ni} * x_{nj},
where y_{ni} is the ith component of the vector y_n.
NAME: calcR
POST: R is now defined
3. Calculate RtR (R-transpose * R).
NAME: calcRtR
POST: RtR is now defined
4. Calculate the corresponding eigenpairs for RtR, and sort them accordingly:
m1 >= m2 >= m3; set v3 = v1 x v2 to ensure a RHS
NAME: calcEigenPairs
POST: The eigen pairs are calculated, sorted such that m1 >= m2 >= m3 and
v3 = v1 x v2.
5. Calculate R*v_k and normalize the first two vectors to obtain b_1, b_2 and set
b_3 = b_1 x b_2. This also takes care of m1 > m2 = 0.
NAME: calcBVectors
POST: b-Vectors are defined and returned
6. Calculate U=(u_{ij})=(sum n b_{ki} * a_{kj}) to obtain the best rotation. Set
sigma_3 = -1 if b3(Ra3) < 0 else sigma_3 = +1.
NAME: calcU
POST: U is defined
7. Calculate the RMSD. The residual error is then
The E = E0 - sqrt(m1) - sqrt(m2) - sigma_3(sqrt(m3)).
NAME: calcRMSD
POST: RMSD is computed.
@note: This should be a static method that takes three parameters
1. The first protein's coordinates, f. This program will
accept coordinates in the form an array of 3D vectors/lists
2. The second protein's coordinates, g.
3. The array of integer pairs representing the pairs to align.
Coordinates should be formatted as as array of 2D vectors/lists.
"""
def __init__(self):
"""
Constructor. @see kabsch.align.
"""
#
# Instance Variables: All three of these will be updated
# every time the user calls ~.align. Just to warn ya'.
#
# U, the rotation matrix
self.U = []
# T, the translation vector
self.T = []
# R, the RMSD
self.R = -1.0
#self.menuBar.addmenuitem('Plugin', 'command', 'Kabsch Align', label = "Align Selections to Optial RMSD", command = lamda s=self: fetchPDBDialog(s))
def align(self, c1, c2, pairs):
"""
Finds the best alignment of c1 and c2's pairs resulting in
the smallest possible RMSD.
@note:
- All weights in this first version are set to 1. Kabsch allows,
differential weighting. In the future, I may extend to this option,
and then pairs may become 3D (r1, r2, weight) or I may add another
parameter.
- Helper functions will soon be provided such that the user may
just use this package alone to compute the rotation.
@param c1: coordinats of the first vectors, as an array of 3D vectors.
@type c1: Python list
@param c2: coordinates of the second set of vectors, as an array of 3D vectors.
@type c2: Python list
@param pairs: the list of pairs as an array of 2D pairs.
@type pairs: Python list of 2D lists.
@return: U, the rotation matrix that gives the optimal rotation between the two proteins.
T, the translation vector given to align the two objects centers of mass.
R, the RMSD of the final rotation.
"""
#
# First we move the center of mass of one protein, to the
# center of mass of the other. This removes any translation
# between the two.
#
T1, T2, c1, c2 = self.superpose(c1, c2)
# Calculate the initial RMSD
E0 = self.calcE0(c1, c2)
# Calculate R via eq. 7.
R = self.calcR(c1, c2)
# Calculate R(transpose)*R
RtR = self.calcRtR(R)
# Determined the eigenpairs for the matrix RtR.
eValues, eVectors = self.calcEigenPairs(RtR)
# Determine the bVectors as required
bVectors = self.calcBVectors(R, eVectors)
# Calculate the roation matrix
U = self.calcU(eVectors, bVectors)
# Calculate the final RMSD using U.
RMSD = self.calcRMSD(E0, eValues, eVectors, bVectors, R, len(c1))
return U, T1, T2, RMSD, c1, c2
def superpose(self, c1, c2 ):
"""
Calculate the center of mass for each protein. Then, move the protein
to its center of mass. We choose as a convention, to use the origin as
the center of mass of the first set of coordinates. This will allow us to
return one translation vector, instead of two.
(CORRECT)
@precondition: c1 and c2 are well defined lists of N-dimensional points with length > 0.
@postcondition: T is now defined.
@param c1: coordinats of the first vectors, as an array of 3D vectors.
@type c1: Python list
@param c2: coordinates of the second set of vectors, as an array of 3D vectors.
@type c2: Python list
@return: T the translation vector.
c2 one list of coordinates that of c2 translated to the COM of c1.
"""
# make sure we don't get bad data
if len(c1) != len(c2):
print "Two different length selections, with lengths, %d and %d." % (len(c1), len(c2))
print "This algorithm must be used with selections of the same length."
print "In PyMol, type 'count_atoms sel1' where sel1 are your selections to find out their lengths."
print "Example: optAlign MOL1 and i. 20-40, MOL2 and i. 102-122"
print "Example 2: optAlign 1GGZ and i. 4-146 and n. CA, 1CLL and i. 4-146 and n. CA"
assert len(c1) == len(c2) != 0
L = len(c1)
#
# Centers of Mass
#
c1COM = Numeric.zeros((3,1), Numeric.Float64)
c2COM = Numeric.zeros((3,1), Numeric.Float64)
# calculate the CsOM
for i in range(L):
for j in range(3):
c1COM[j] += c1[i][j]
c2COM[j] += c2[i][j]
T1 = - c1COM / L
T2 = - c2COM / L
# move everything back to the origin.
for i in range(L):
for j in range(3):
c1[i][j] += T1[j]
c2[i][j] += T2[j]
return T1, T2, c1, c2
def calcR( self, c1, c2 ):
"""
Calculate the matrix, R, by (eq7, 1976). M{r_{i,j} = sum_n w_n * y_{ni} * x_{nj}},
where M{y_{ni}} is the ith component of the vector M{y_n}.
(CORRECT)
@param c1: coordinates of the first vectors, as an array of 3D vectors.
@type c1: Python list
@param c2: coordinates of the second set of vectors, as an array of 3D vectors.
@type c2: Python list
@postcondition: R is now defined.
@return: R
@rtype : 3x3 matrix
"""
# Create the 3x3 matrix
R = Numeric.zeros((3,3), Numeric.Float64)
L = len(c1)
for k in range(L):
for i in range(3):
for j in range(3):
R[i][j] += c2[k][i] * c1[k][j]
# return R the 3x3 PSD Matrix.
return R
def calcRtR( self, R ):
"""
Calculate RtR (R-transpose * R).
(CORRECT)
@param R: Matrix
@type R: 3x3 Matrix
@precondition: R is a the well formed matrix as per Kabsch.
@postcondition: RtR is now defined
@return: M{R^tR}
@rtype : 3x3 matrix
"""
RtR = Numeric.matrixmultiply(Numeric.transpose(R), R)
return RtR
def calcEigenPairs( self, RtR ):
"""
Calculate the corresponding eigenpairs for RtR, and sort them accordingly:
M{m1 >= m2 >= m3}; set M{v3 = v1 x v2} to ensure a RHS
(CORRECT)
@postcondition: The eigen pairs are calculated, sorted such that M{m1 >= m2 >= m3} and
M{v3 = v1 x v2}.
@param RtR: 3x3 Matrix of M{R^t * R}.
@type RtR: 3x3 Matrix
@return : Eigenpairs for the RtR matrix.
@rtype : List of stuff
"""
eVal, eVec = LinearAlgebra.eigenvectors(RtR)
# This is cool. We sort it using Numeric.sort(eVal)
# then we reverse it using nifty-crazy ass notation [::-1].
eVal2 = Numeric.sort(eVal)[::-1]
eVec2 = [[],[],[]] #Numeric.zeros((3,3), Numeric.Float64)
# Map the vectors to their appropriate owners
if eVal2[0] == eVal[0]:
eVec2[0] = eVec[0]
if eVal2[1] == eVal[1]:
eVec2[1] = eVec[1]
eVec2[2] = eVec[2]
else:
eVec2[1] = eVec[2]
eVec2[2] = eVec[1]
elif eVal2[0] == eVal[1]:
eVec2[0] = eVec[1]
if eVal2[1] == eVal[0]:
eVec2[1] = eVec[0]
eVec2[2] = eVec[2]
else:
eVec2[1] = eVec[2]
eVec2[2] = eVec[0]
elif eVal2[0] == eVal[2]:
eVec2[0] = eVec[2]
if eVal2[1] == eVal[1]:
eVec2[1] = eVec[1]
eVec2[2] = eVec[0]
else:
eVec2[1] = eVec[0]
eVec2[2] = eVec[1]
eVec2[2][0] = eVec2[0][1]*eVec2[1][2] - eVec2[0][2]*eVec2[1][1]
eVec2[2][1] = eVec2[0][2]*eVec2[1][0] - eVec2[0][0]*eVec2[1][2]
eVec2[2][2] = eVec2[0][0]*eVec2[1][1] - eVec2[0][1]*eVec2[1][0]
return [eVal2, eVec2]
def calcBVectors( self, R, eVectors ):
"""
Calculate M{R*a_k} and normalize the first two vectors to obtain M{b_1, b_2} and set
M{b_3 = b_1 x b_2}. This also takes care of {m2 > m3 = 0}.
(CORRECT)
@postcondition: b-Vectors are defined and returned
@return: The three B-vectors
@rtype: List of 3D vectors (Python LOL).
"""
bVectors = Numeric.zeros((3,3), Numeric.Float64)
for i in range(3):
bVectors[i] = Numeric.matrixmultiply(R, eVectors[i])
bVectors[0] = bVectors[0] / Numeric.sqrt(Numeric.add.reduce(bVectors[0]**2))
bVectors[1] = bVectors[1] / Numeric.sqrt(Numeric.add.reduce(bVectors[1]**2))
bVectors[2] = bVectors[2] / Numeric.sqrt(Numeric.add.reduce(bVectors[2]**2))
bVectors[2][0] = bVectors[0][1]*bVectors[1][2] - bVectors[0][2]*bVectors[1][1]
bVectors[2][1] = bVectors[0][2]*bVectors[1][0] - bVectors[0][0]*bVectors[1][2]
bVectors[2][2] = bVectors[0][0]*bVectors[1][1] - bVectors[0][1]*bVectors[1][0]
return bVectors
def calcU( self, eVectors, bVectors ):
"""
Calculate M{U=(u_{ij})=(sum n b_{ki} * a_{kj})} to obtain the best rotation. Set
M{sigma_3 = -1 if b3(Ra3) < 0 else sigma_3 = +1}.
(CORRECT)
@postcondition: U is defined
@param eVectors: Eigenvectors for the system.
@type eVectors: Eigenvectors
@param bVectors: BVectors as described by Kabsch.
@type bVectors: BVectors
@return: U the rotation matrix.
@rtype :3x3 matrix.
"""
U = Numeric.zeros((3,3), Numeric.Float64)
for k in range(3):
for i in range(3):
for j in range(3):
U[i][j] += Numeric.matrixmultiply(bVectors[k][i], eVectors[k][j])
return U
def calcE0( self, c1, c2 ):
"""
Calculates the initial RMSD, which Kacbsch called E0.
(CORRECT)
@param c1: coordinats of the first vectors, as an array of 3D vectors.
@type c1: Python list
@param c2: coordinates of the second set of vectors, as an array of 3D vectors.
@type c2: Python list
@return: E0 the initial RMSD.
@rtype : float.
"""
E0 = 0.0
L = len(c1)
for i in range( L ):
for j in range(3):
E0 += 0.5*( c1[i][j]*c1[i][j]+c2[i][j]*c2[i][j])
return E0
def calcRMSD( self, E0, eValues, eVectors, bVectors, R, N):
"""
Calculate the RMSD. The residual error is then
The M{E = E0 - sqrt(m1) - sqrt(m2) - sigma_3(sqrt(m3))}.
@param E0: Initial RMSD as calculated in L{calcE0}.
@type E0: float.
@param eVectors: Eigenvectors as calculated from L{calcEigenPairs}
@type eVectors: vectors, dammit!
@param bVectors: B-vectors as calc. from L{calcBVectors}
@type bVectors: More vectors.
@param R: The matrix R, from L{calcR}.
@type R: 3x3 matrix.
@param N: Number of equivalenced points
@type N: integer
@postcondition: RMSD is computed.
@return: The RMSD.
"""
sigma3 = 0
if Numeric.matrixmultiply(bVectors[2], Numeric.matrixmultiply( R, eVectors[2])) < 0:
sigma3 = -1
else:
sigma3 = 1
E = math.sqrt( 2*(E0 - math.sqrt(eValues[0]) - math.sqrt(eValues[1]) - sigma3*(math.sqrt(eValues[2]))) / N)
return E
def calcSimpleRMSD( self, c1, c2 ):
"""
Calculates the usual concept of RMSD between two set of points. The CalcRMSD above
sticks to Kabsch's alignment method protocol and calculates something much different.
@see kabsch.calcRMSD
@param c1: List of points #1
@type c1: LOL
@param c2: List of points #2
@type c2: LOL
@return: RMSD between the two
"""
RMSD = 0.0
for i in range(len(c1)):
for j in range(3):
RMSD += (c2[i][j]-c1[i][j])**2
RMSD = RMSD / len(c1)
RMSD = Numeric.sqrt(RMSD)
return RMSD
#####################################################################
#
# UTIL Functions
def rotatePoints(self, U, c2):
"""
Rotate all points in c2 based on the rotation matrix U.
@param U: 3x3 Rotation matrix
@type U: 3x3 matrix
@param c2: List of points to rotate
@type c2: List of 3D vectors
@return: List of rotated points
"""
L = len(c2)
for n in range(L):
c2[n][0] = c2[n][0] * U[0][0] + c2[n][1] * U[1][0] + c2[n][2] * U[2][0]
c2[n][1] = c2[n][0] * U[0][1] + c2[n][1] * U[1][1] + c2[n][2] * U[2][1]
c2[n][2] = c2[n][0] * U[0][2] + c2[n][1] * U[1][2] + c2[n][2] * U[2][2]
return c2
def writeU( self, U, fileName ):
"""
Convenience function. Writes U to disk.
"""
if len(fileName) == 0:
fileName = "./U"
outFile = open( fileName, "wb")
for i in range(3):
for j in range(3):
outFile.write( str(U[i][j]).ljust(20) )
outFile.write("\n")
outFile.close()
def optAlign( sel1, sel2 ):
"""
optAlign performs the Kabsch alignment algorithm upon the alpha-carbons of two selections.
Example: optAlign MOL1 and i. 20-40, MOL2 and i. 102-122
Example 2: optAlign 1GGZ and i. 4-146 and n. CA, 1CLL and i. 4-146 and n. CA
Two RMSDs are returned. One comes from the Kabsch algorithm and the other from
PyMol based upon your selections.
By default, this program will optimally align the ALPHA CARBONS of the selections provided.
To turn off this feature remove the lines between the commented "REMOVE ALPHA CARBONS" below.
@param sel1: First PyMol selection with N-atoms
@param sel2: Second PyMol selection with N-atoms
"""
cmd.reset()
# make the lists for holding coordinates
# partial lists
stored.sel1 = []
stored.sel2 = []
# full lists
stored.mol1 = []
stored.mol2 = []
# now put the coordinates into a list
# partials
# -- REMOVE ALPHA CARBONS
sel1 += " and N. CA"
sel2 += " and N. CA"
# -- REMOVE ALPHA CARBONS
cmd.iterate_state(1, selector.process(sel1), "stored.sel1.append([x,y,z])")
cmd.iterate_state(1, selector.process(sel2), "stored.sel2.append([x,y,z])")
# full molecule
mol1 = cmd.identify(sel1,1)[0][0]
mol2 = cmd.identify(sel2,1)[0][0]
cmd.iterate_state(1, mol1, "stored.mol1.append([x,y,z])")
cmd.iterate_state(1, mol2, "stored.mol2.append([x,y,z])")
K = kabsch()
U, T1, T2, RMSD, c1, c2 = K.align(stored.sel1, stored.sel2, [])
stored.mol2 = map(lambda v:[T2[0]+((v[0]*U[0][0])+(v[1]*U[1][0])+(v[2]*U[2][0])),T2[1]+((v[0]*U[0][1])+(v[1]*U[1][1])+(v[2]*U[2][1])),T2[2]+((v[0]*U[0][2])+(v[1]*U[1][2])+(v[2]*U[2][2]))],stored.mol2)
#stored.mol1 = map(lambda v:[ v[0]+T1[0], v[1]+T1[1], v[2]+T1[2] ], stored.mol1)
stored.mol1 = map(lambda v:[ v[0]+T1[0], v[1]+T1[1], v[2]+T1[2] ], stored.mol1)
cmd.alter_state(1,mol1,"(x,y,z)=stored.mol1.pop(0)")
cmd.alter_state(1,mol2,"(x,y,z)=stored.mol2.pop(0)")
cmd.alter( 'all',"segi=''")
cmd.alter('all', "chain=''")
print "RMSD=%f" % cmd.rms_cur(sel1, sel2)
print "MY RMSD=%f" % RMSD
cmd.hide('everything')
cmd.show('ribbon', sel1 + ' or ' + sel2)
cmd.color('gray70', mol1 )
cmd.color('paleyellow', mol2 )
cmd.color('red', 'visible')
cmd.show('ribbon', 'not visible')
cmd.center('visible')
cmd.orient()
cmd.zoom('visible')
cmd.extend("optAlign", optAlign)
References
[Kabsch, 1976] Kabsch, W. (1976). A solution for the best rotation to relate two sets of vectors. Acta. Crystal, 32A:922-923.
[Kabsch, 1978] Kabsch, W. (1978). A discussion of the solution for the best rotation to related two sets of vectors. Acta. Crystal, 34A:827-828.